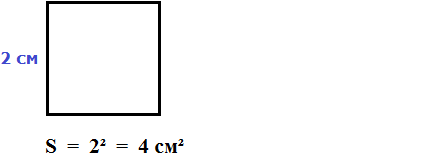
Способы определения площади земельного участка

Виды треугольников

Треугольник представляет собой многоугольник, который имеет три стороны и может быть отнесен к следующим типам:

• Равносторонний треугольник имеет равные стороны и равные углы.
• Равнобедренный треугольник имеет две равные стороны и два равных угла.
• Разносторонний треугольник имеет три неравные стороны и три неравных угла.
• Прямоугольный треугольник имеет один прямой угол 90 градусов.
• Остроугольный треугольник имеет все углы меньше 90 градусов.
• Тупоугольный треугольник имеет один угол больше 90 градусов.

Площадь любого треугольника определяется по формулам.

1. Как рассчитать площадь треугольника, если известны высота и основание треугольника:

• S=1⁄2×a×h, где: h – высота, a — основание.
• S=1⁄2xa×b×sinα, где: a, b – любые две стороны, α — угол между ними.
• S=p×r, где: p = (a+b+c) / 2 — полупериметр, a, b, c – три стороны, r – радиус круга.

Площадь равностороннего треугольника:

S=a2х√3 ⁄4 , где a=b= c.

Площадь равнобедренного треугольника:

S=1⁄4xbx√(4a2-b2).

2. Как рассчитать площадь треугольника, если заданы две стороны и угол между ними:

S=1⁄2xaxbxsinC=1⁄2xbxcxsinA =1⁄2xaxcxsinB.

Пример 1: Найти S треугольника, сторона которого составляет 14 см, а высота — 10 см.

Решение: b=14 см, h=10 см, A=1⁄2х14х10=70

Ответ: 70 см2.

Пример 2. Найти область треугольника, стороны которого и угол между ними заданы следующим образом: a=5 см и b=7 см, C=45 градусов.

Решение: Площадь треугольника =1⁄2xaxbxsin 45.

Площадь =1⁄2×5×7×0,707 (поскольку sin45=0,707)

Площадь =1⁄2×24,745=12,3725

Ответ: 12,3725 см2.

Пример 3. Найдите площадь (в м2) равнобедренного треугольника, стороны которого составляют 10 м, а основание — 12 м.

Решение: Площадь равнобедренного треугольника определяется:

A=1⁄4xbx√(4a2-b2)A=1⁄4х12х√(4х(10)2-(12)2)А=48

Ответ: 48 м2.

Пример 4. Найти площадь треугольника, стороны которого равны 8, 9 и 11 соответственно. Все единицы измерения даны в метрах (м).

Решение: Стороны a=8, b=9 и c=11. Согласно формуле Херона площадь треугольника может быть определена по следующей формуле: A=√(sx(sa)х(sb)х(sc)). Прежде всего нам нужно определить s, которая является полупериметром треугольника: s =1⁄2х(a+b+c)=1⁄2х(8+9+11)=14.

Теперь, вставив значение полупериметра в формулу Герона, можно определить площадь треугольника: A=√(sx(sa)х(sb)х(sc)). A=√(14х(14-8)х(14-9)х(14-11)). A=√(1260)=35,50

Ответ: 35,50 м2.

Для чего необходимо знать площадь комнаты и что потребуется для расчетов?

В каких же случаях необходимо рассчитывать площадь комнаты?

Конечно, в первую очередь для определения количества расходных материалов для ремонта. Многие закупают их с запасом, а излишки возвращают в магазин. Однако в данном случае теряется много времени, к тому же не все магазины предоставляют такую услугу. Поэтому целесообразней правильно высчитать площадь всех поверхностей перед покупками.

Чтобы у вас не осталось много обрезков, правильно рассчитайте площадь стен, которые требуют оклейки

• Кроме того, зная площадь, проще распланировать свой бюджет. Ведь даже стоимость работ наемных работников в большинстве случаев зависит от того, сколько квадратных метров они должны обработать.
• Количество осветительных приборов также зависит от площади. Однако в большинстве случаев к сложным расчетам при выборе светильников не прибегают, данный вопрос обычно решается опытным путем.

Пример недостаточного освещения в ванной комнате

И последнее. Одна из главных величин в квартире – объем помещений (при этом необходимо площадь умножить на высоту), ведь в зависимости от него подбирают климатическое оборудование.

Мощность кондиционера в первую очередь зависит от объема помещения

Таким образом, существует огромное количество причин, по которым необходимо правильно высчитать площадь помещения. Но с чего же начать? Сначала нужно подготовить измеряемое помещение и инструменты.

Измерения желательно проводить в полностью освобожденном помещении. Если такой возможности нет, расчистите хотя бы участки около стен, ведь именно вдоль них будут проводиться замеры.

Обязательно отодвиньте всю крупную мебель от стен, которые вы будете измерять

Итак, для определения площади помещения необходимы следующие приспособления:

1. Рулетка. Конечно, электронное приспособление удобней, но оно имеет большую погрешность. Кроме того, такой рулеткой не измерить сложные формы, при работе с выступающими элементами также могут возникнуть проблемы. Поэтому оптимальный набор – простая рулетка и линейка. Главное – проверить их точность, так как многие старые или детские приспособления имеют приличную погрешность.
2. Карандаш.
3. Листок бумаги для вычислений и записи результатов.
4. Калькулятор.

Кроме того, вам может понадобиться длинная линейка для проверки ровности стен.

Как посчитать квадратные метры комнаты

В каких случаях требуется квадратура помещения:

• При установке на кухню модуля из шкафов.
• При оплате коммунальных услуг, где сумма рассчитывается исходя из метража.
• При оплате рабочим после ремонта. Их тарифы также привязаны к площадям и количеству метров.
• При определении нормативов освещения вычисляется площадь.
• При установке отопления, вентиляции и кондиционирования требуется знать объем (кубатуру) помещения. Он вычисляется с помощью величины площади.
• При расчете количества закупаемых материалов для планируемого ремонта.

Чтобы правильно высчитать необходимые величины нужно знать несколько формул и уметь с их помощью рассчитать квадратные метры стен, потолка и пола.

Квадратура помещения нужна при оплате коммунальных услуг, определении нормативов освещения, установке отопления и покупке материалов для ремонта.

Для этого потребуются простейшие инструменты:

• Рулетка. Механическая, размером от 3 до 5 метров. Ею измерять лучше вдвоем, чтобы избежать погрешностей. Минимальная единица измерения – миллиметр. Электронная, измеряет лазерным лучом. Получить измерительную величину можно просто направив луч в начальную точку. Единица измерения здесь – миллиметр или сантиметр.

  Некоторые «умные» рулетки могут сразу высчитывать площадь помещения, не измеряя дополнительно что-то. С измерениями такой рулеткой можно справиться в одиночку, без дополнительной помощи. Плюс в быстроте измерений и расчетов. Минус в дороговизне и проблемах с измерением неправильных помещений.

• Калькулятор. Также для удобства в расчетах разработаны специальные компьютерные программы.
• Угольник строительный. Должен быть с длинными сторонами – в этом случае замеры получатся более точными.
• Блокнот или тетрадь для занесения всех схем, измерений, расчетов.
• Уровень. С его помощью можно рассчитать отклонения вертикали/горизонтали.

Прежде чем приступить к измерениям и расчетам, нужно подготовить все необходимые инструменты.

1. Первое, что нужно сделать – это узнать, как рассчитывается квадратный метр. Здесь пригодится рулетка со шкалой в сантиметрах и метрах.
2. Затем измеряется длина помещения и его ширина. Причем, ширина измеряется, прикладывая рулетку строго перпендикулярно длине.
3. Измерения записываются вплоть до сантиметра. В сторону метров округлять не стоит.

Для измерения размеров помещения нужна обычная рулетка. Но существуют и “умные рулетки”. Они могут сразу высчитывать общую площадь.

Чтобы рассчитать квадраты на калькуляторе, нужно измеренную величину записать следующим образом: 1м=0.01 см. Если предположить, что длина комнаты – 3 метра 56 см, то на калькуляторе набрать 3,56. То же самое касается и ширины. В итоге, умножить длину комнаты на ее же ширину и получить величину квадратуры измеряемого помещения.

Для расчетов вам понадобится калькулятор и знание формул.

Для того, чтобы корректно измерить помещение, желательно освободить хотя бы две ее стороны от мебели и лишних предметов. В этом случае идеально измерять комнату на стадии ремонта.

Рулетка должна хорошо прилегать к измеряемой поверхности. Длину требуется измерить вдоль стены (или стен, если форма измеряемой фигуры не правильная). В начале измерений лучше проверить прямоугольность, измерив рулеткой диагонали помещения и сравнив цифры. Таким образом уточняется правильность формы.

Можно воспользоваться лазерной рулеткой. Такие дальномеры стали незаменимыми помощниками специалистов и умеют запоминать измерения и вычислять по ним площадь или кубатуру помещения.

А вот чтобы проверить прямые линии понадобится уровень. Реже большой строительный угольник или самодельный циркуль.

Уровень – инструмент для оценки соответствия поверхностей вертикальной и горизонтальной плоскости относительно земли.

Расчеты можно сразу переносить на схему. Обязательно измерять помещение несколько раз, во избежание ошибок. Во время замеров быть внимательным и собранным, следить абсолютно за всеми мелочами, которые могут повлиять на величины.

Площадь комнаты можно вычислить с помощью простой школьной формулы:

S=A*B.

• S – площадь;
• A – длина;
• B – ширина.

Подобным же образом можно вычислить и площадь каждой стены, пола и потолка.
В случае если помещение треугольной формы – нужно измерить длину и ширину, умножить друг на друга и разделить на 2.

Или по формуле:

S = (А*В)/2.

Площадь комнаты можно вычислить с помощью простой школьной формулы.

Как рассчитать площадь комнаты – пошаговая инструкция

При расчете площади нужно знать длину, ширину и высоту комнаты

Можно, конечно, заглянуть в техническую документацию дома и посмотреть в ней все нужные характеристики. Но, во-первых, там нередко бывают ошибки, во-вторых, иногда проще вычислить всё самостоятельно, чем найти документы.

Для проведения подсчётов нам понадобятся определённые инструменты, большинство из которых можно запросто найти в каждом доме. А именно:

• рулетка;
• карандаш;
• бумага для записей;
• калькулятор (можно использовать калькулятор, который размещён на нашем сайте);
• трезвость ума и ясность мыслей.

Пол

Чтобы высчитать квадратуру пола в прямоугольной или квадратной комнате, необходимо узнать её длину и ширину.

Проводить замеры лучше у основания стен, а для этого желательно отодвинуть или вынести всю мебель. Но, если такая процедура в ваши планы не входила, можно мерить и по центру. Главное при этом, чтобы воображаемая линия, по которой будет производиться измерение, располагалась под углом в 90° к стене.

После того как данные замеров получены и проверены, их нужно перемножить по формуле , где S — площадь в квадратных метрах, a и b — длина и ширина, соответственно.

Если к основному помещению прилегает ниша или какое-нибудь другое — его площадь необходимо вычислить по тому же алгоритму, и результаты приплюсовать к площади комнаты. Если есть различные выступы, которые занимают его часть — их также следует измерить и полученный результат вычесть из общего.

С квадратами и прямоугольниками всё просто. А как посчитать S комнаты, если она имеет неправильную форму? Здесь придётся применить логическое мышление, и немного вспомнить школьный курс алгебры и геометрии. Но давайте по порядку.

Если помещение неправильной формы

Постарайтесь мысленно или на бумаге разделить комнату на простые элементы (квадраты, прямоугольники, треугольники). Далее, нужно будет высчитать размеры каждого из них, и результаты сложить.

• для треугольника — . Где a — длинна основания треугольника, b — высота, проведённая от вершины к основанию;
• для круга — . Где 3,14, r — радиус круга (чтобы узнать радиус — найдите с помощью рулетки самое длинное расстояние между стенами и разделите его на 2);
• для полукруга — (буквенные обозначения совпадают с предыдущим пунктом).

Как оказалось, и в таком случае ничего сложного нет. Главное, тщательно проверять результаты замеров, чтобы в расчёты не закралась случайная ошибка, и их не пришлось производить заново.

И ещё. Если вы хотите произвести монтаж тёплого пола, не забудьте отдельно вычислить площадь, которую занимает мебель, и вычтите её из общего значения для помещения.

С полом мы разобрались. Но при подготовке, допустим, к переклеиванию обоев это вам мало чем поможет. Нужно будет узнать точное количество квадратных метров, которое занимают  стены.

Стены

Площадь каждой отдельно взятой стены можно высчитать так же, как и квадратуру пола. Только теперь вместо ширины помещения нужно будет измерить её высоту. Множим длину стены на высоту и получаем необходимый нам результат в квадратных метрах.

Измерение высоты лазерной рулеткой

А можно вычислить и для всех стен сразу. Для этого вам понадобится узнать периметр пространства. Возьмите рулетку и измерьте длину каждой стены, результаты сложите — это и будет периметр. Остаётся измерить высоту комнаты и воспользоваться следующей формулой: , где p — периметр, а h — высота.

Теперь необходимо разобраться с оконными, дверными и прочими проёмами, присутствующими в помещении.

Точнее, рассчитать площадь каждого из них (по формулам, представленным выше, в зависимости от формы проёма), результаты суммировать и вычесть из общего количества.

Существует также ряд общих рекомендаций по проведению замеров.

[править] Обозначения

Введём обозначения:

a — первая сторона;

b — вторая сторона;

c — третья сторона;

d — четвёртая сторона;

α — угол между сторонами a и b;

β — угол между сторонами b и c;

γ — угол между сторонами c и d;

η — угол между сторонами a и d;

d₁ — диагональ, соединяющая вершины углов α и γ;

d₂ — диагональ, соединяющая вершины углов β и η;

l₁ — средняя линия, соединяющая середины сторон a и c;

l₂ — средняя линия, соединяющая середины сторон b и d;

φ — угол (острый) между диагоналями;

ψ — угол (острый) между средними линиями;

p — полупериметр четырёхугольника;

S_Δ — площадь треугольника;

S_четыр — площадь четырёхугольника.

Погрешность определения площади

При определении площадей участков возникают неточности, которые характеризуются погрешностями. Погрешность — это разность между вычисленной величиной площади участка и ее истинной величиной.

Для различных методов определения площади такие погрешности могут быть различными.

Для аналитического метода точность расчета площади зависит исключительно от погрешностей, связанных с измерением координат поворотных точек. При этом, средняя квадратическая погрешность (СКП) аналитического метода расчета (mp) определяется формулой:

mp= mt*√ P, где:

• mt — СКП расположения поворотных точек;
• P — площадь участка.

Для примера можно взять допустимые при межевании точности mt, которые определены соответствующими нормативными актами (например, Приложением к приказу МЭР № 518). Эти точности зависят от типа земель.

Так, для населенных пунктов этот показатель равен 10 см, а для дачных участков и садоводств-20 см. Таким образом, для садового участка в 600 кв. м точность определения площади аналитическим методом может составить:

mpс= 0,2*√600=4,89 м.

При реализации графического метода на его точность влияют погрешности измерений, погрешности составления плана, деформация бумаги. Относительная погрешность такого метода составляет от 1:500 до 1:1000.

Точность механического метода также зависит от погрешностей составления плана (или карты), состояния бумаги, на которой нанесен план участка. Кроме того, на точность этого метода влияет размер участка. Этот метод не рекомендуется применять для участков размером менее 10-12 см2.

В благоприятных условиях относительная погрешность измерений площади планиметром может достигать 1:400.

Мы расскажем вам о том как взять земельный участок в аренду с правом выкупа.

При покупке квартиры можно получить налоговый вычет. Подробнее об этом читайте в нашей статье.

Хотите оформить в собственность участок, взятый в аренду на 49 лет? Здесь есть подробная инструкция.

Формулы для нахождения площади

Через две стороны

Площадь прямоугольника через две стороны можно вычислить по формуле:

\(S=ab\)

где a, b — соседние стороны прямоугольника.

Через диагонали и синус угла между ними

Для того, чтобы найти площадь прямоугольника через диагонали и синус угла, нужно воспользоваться формулой:

\(S=\frac{d^2\sin\alpha}2\)

где \(d \) — диагональ, \(\alpha\) — угол между диагоналями (острый).

Через любую сторону и диагональ

Чтобы определить площадь прямоугольника через любую сторону и диагональ, нужно воспользоваться формулой:

\(S=a\sqrt{d^2-a^2}=b\sqrt{d^2-b^2}\)

где a, b — соседние стороны прямоугольника, d — диагональ.

Через сторону и диаметр описанной окружности

Чтобы узнать площадь прямоугольника через сторону и диаметр описанной окружности, нужно воспользоваться формулой:

\(S=a\sqrt{D^2-a^2}=b\sqrt{D^2-b^2}\)

где a, b — соседние стороны прямоугольника, D — диаметр описанной окружности.

Через сторону и радиус описанной окружности

Вычисление площади прямоугольника через сторону и радиус описанной окружности происходит по формуле:

\(S=a\sqrt{4R^2-a^2}=b\sqrt{4R^2-b^2}\)

где a, b — соседние стороны прямоугольника, R — радиус описанной окружности.

Через сторону и периметр

Чтобы посчитать площадь прямоугольника через сторону и периметр, нужно воспользоваться формулой:

\(S=\frac{Pa-2a^2}2=\frac{Pb-2b^2}2\)

где a, b — соседние стороны прямоугольника, Р — периметр.

Через радиус описанной окружности и синус угла между диагоналями

Способ нахождения площади прямоугольника через радиус окружности и синус угла между диагоналями происходит по формуле:

\(S=\frac{4R^2\sin\alpha}2\)

Формулы площади выпуклого четырехугольника

1. Формула площади четырехугольника по длине диагоналей и углу между ними
   Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

   S =	1	1 2 sin
   2

   где S — площадь четырехугольника,₁, ₂ — длины диагоналей четырехугольника, — угол между диагоналями четырехугольника.

2. Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
   Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружностиS =  · 

3. Формула площади четырехугольника по длине сторон и значению противоположных угловS = √()()()() —  cos2

   где S — площадь четырехугольника,, , , — длины сторон четырехугольника,

   =	+  +  +	— полупериметр четырехугольника,
   2

   =	+	— полусумма двух противоположных углов четырехугольника.
   2

4. Формула площади четырехугольника, вокруг которого можно описать окружностьS = √()()()()

Формулы площади параллелограмма

1. Формула площади параллелограмма по длине стороны и высотеПлощадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = 

2. Формула площади параллелограмма по двум сторонам и углу между нимиПлощадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = 

3. Формула площади параллелограмма по двум диагоналям и углу между нимиПлощадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

   S =	1	12
   2

   где S — Площадь параллелограмма, — длины сторон параллелограмма, — длина высоты параллелограмма,₁, ₂ — длины диагоналей параллелограмма, — угол между сторонами параллелограмма, — угол между диагоналями параллелограмма.

Методика выполнения работы

Перед тем, как рассчитать квадратуру дома, нужно подготовить следующее:

1. Калькулятор для проведения вычислений. 
2. Рулетка для проведения измерений. При этом надо учитывать, что некоторые производят измерения в дюймах – они не подойдут. Нужна рулетка, которая указывает длину с помощью сантиметров. 
3. Потребуется план квартиры. Измерение площади стен, пола и потолка будет выполняться на его основе. Если такую схему найти нельзя, то её нужно нарисовать от руки, стремясь реалистично отобразить размеры и геометрическую форму частей. 
4. Также потребуется бумага и карандаш для ведения записей в процессе работы. 

При замерах полов, стен и потолков в первую очередь потребуются знания из школьной геометрии. Простейшим способом, как рассчитать площадь дома в квадратных метрах, является вычисление прямоугольных поверхностей. Площадь прямоугольника вычисляется как произведение его сторон. 

Вычисление площади простейших геометрических фигур основано на базовых формулах из геометрииИсточник stroychik.ru

При этом важно учитывать следующее.

Хотя на вид комната состоит из прямоугольных деталей, на самом деле это может оказаться немного по-другому. Например, ширина стен, измеренная с одной и другой стороны, может отличаться на несколько сантиметров. Эта проблема особенно существенна при измерении расстояний в домах старой постройки. В таких случаях обычно измеряют длину в нескольких местах, а при вычислении площади используют среднее значение. 
Вычисления позволяют получить нужные цифры с высокой точностью

Однако будет разумной предосторожностью при вычислениях добавить к площади небольшую величину. Это позволит исключить ситуацию, в которой стройматериалов чуть-чуть не хватило. 

Таким способом можно вычислить площадь прямоугольных пустых стен, пола и потолка.
 

Сложная форма стен и потолка может быть разделена на простые фигуры для упрощения вычисленийИсточник www.buvbaze.lv

Расчёт площади стен с окнами и дверьми

Если на стене есть окно или дверь, то вычисление производится следующим образом:

• Определяется площадь стены без учёта двери или окна. 
• Вычисляется площадь каждого окна или двери путём умножения их длины на ширину. 
• Из площади стены вычитают площадь окон и дверей. 

Этот способ применим в тех случаях, когда рассматриваются прямоугольные стены.

Площадь стены, имеющей неправильную форму

В этом случае нужно разделить вычисления на этапы. Стена с нишами может иметь сложную форму. Однако её всегда можно условно разбить на несколько участков, каждый из которых соответствует одной из простых форм. Затем надо рассчитать площади каждой из частей и сложить их. 

Как посчитать площадь стен, рассказано в видео

Расчёт через периметр

Если комната имеет неправильную форму, то площадь стен можно вычислить, измерив длину периметра. В этом случае проводят измерение горизонтальных отрезков по каждой из сторон помещения и складывают их вместе, затем определяют высоту. Произведение этих величин равно площади стен в этом помещении. 

Несколько советов

• Нужно при проведении расчётов все цифры наносить на план. Таким образом сохранится не только результат, но и промежуточные вычисления, которые могут пригодится при проведении ремонтных работ в будущем. 
• При вычислении площади нужно учитывать, что не всегда необходима полная величина. Например, обои могут клеить не только на всю стену, а на их часть. Класть плитку могут до потолка либо только до определённой высоты. Поэтому нужно точно определить, как высчитать квадратуру дома с учётом конкретного плана ремонта. 

Как сделать замеры – можно посмотреть в видеоролике:

Для того, чтобы точно знать, сколько необходимо стройматериалов для проведения работ, нужно учитывать площади стен, пола и потолка, а также нормы расхода стройматериалов. Среднюю величину расхода можно узнать, спросив у продавцов, а квадратуру дома необходимо измерить самостоятельно. Для этого нужно воспользоваться знаниями из элементарной геометрии. При вычислении площади сложных фигурных поверхностей их разбивают на простые части, делают необходимые вычисления, затем суммируют их. 

Вывод формул для площадей четырехугольников

Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле

где  d1 и d2 – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис. 1).

Рис. 1

Доказательство. В соответствии с рисунком 1 справедливо равенство:

что и требовалось доказать.

Утверждение 2. Площадь параллелограммапараллелограмма можно найти по формуле

S = a ha ,

где a – сторона параллелограмма, а ha – высотавысотавысота, опущенная на эту сторону (рис. 2).

Рис. 2

Доказательство. Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

SABCD = SAEFD = a ha ,

что и требовалось доказать.

Утверждение 3.Площадь параллелограмма параллелограмма можно найти по формуле

S = ab sin φ,

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

Рис. 3

Доказательство. Поскольку

ha = b sin φ,

то, в силу утверждения 2, справедлива формула

S = a ha = ab sin φ,

что и требовалось доказать.

Утверждение 4. Площадь ромбаромба можно найти по формуле

,

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).

Рис. 4

Доказательство. Поскольку каждая из диагоналей ромба является биссектрисой угла, а каждая точка биссектрисы угла равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена от всех сторон ромба и является центром вписанной в ромб окружности. Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому

что и требовалось доказать.

Утверждение 5. Площадь трапеции можно найти по формуле

,

где a и b – основания трапеции, а h  – высотавысотавысота (рис.5).

Рис. 5

Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF. Поэтому

что и требовалось доказать.

Утверждение 6. Площадь трапеции трапеции можно найти по формуле

где a и b – основания, а c и d – боковые стороны трапеции, (рис.6).

Рис. 6

Доказательство. Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

Следовательно,

где

что и требовалось доказать.

Утверждение 7. Площадь дельтоида, дельтоида, можно найти по формуле:

S = (a + b) r,

где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).

Рис. 7

Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.

Если r – радиус вписанной в дельтоид окружности, то

что и требовалось доказать.

На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

У нас также для школьников организованы

Вывод формул для площадей четырехугольников

      Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле

где  d₁ и d₂ – , а φ – любой из четырёх углов между ними (рис. 1).

Рис. 1

      Доказательство. В соответствии с рисунком 1 справедливо равенство:

что и требовалось доказать.

      Утверждение 2. Площадь можно найти по формуле

S = a h_a ,

где a – сторона параллелограмма, а h_a – , опущенная на эту сторону (рис. 2).

Рис. 2

      Доказательство. Поскольку (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

S_ABCD = S_AEFD = a h_a ,

что и требовалось доказать.

      Утверждение 3.Площадь можно найти по формуле

S = ab sin φ,

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

Рис. 3

      Доказательство. Поскольку

h_a = b sin φ,

то, в силу утверждения 2, справедлива формула

S = a h_a = ab sin φ,

что и требовалось доказать.

      Утверждение 4. Площадь можно найти по формуле

,

где r – радиус , а φ – любой из четырёх углов ромба (рис.4).

Рис. 4

      Доказательство. Поскольку каждая из ромба является биссектрисой угла, а . Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому

что и требовалось доказать.

      Утверждение 5. Площадь можно найти по формуле

,

где a и b – основания трапеции, а h  –  (рис.5).

Рис. 5

      Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку , то площадь трапеции ABCD равна площади треугольника ABF. Поэтому

что и требовалось доказать.

      Утверждение 6. Площадь можно найти по формуле

,

где a и b – основания, а c и d – боковые стороны трапеции, (рис.6).

Рис. 6

      Доказательство. Воспользовавшись , составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

      Следовательно,

где

,

что и требовалось доказать.

      Утверждение 7. Площадь , , можно найти по формуле:

S = (a + b) r,

где a и b – неравные стороны дельтоида, а r – радиус (рис.7).

Рис. 7

      Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.

      Если r – радиус вписанной в дельтоид окружности, то

что и требовалось доказать.