Площадь треугольника

Способы нахождения площади

Но существуют также и другие способы, по которым можно найти S этого многоугольника. Рассмотрим основные из них.

Через две стороны и угол

Если вам известны две стороны любого треугольника и угол между ними, найти площадь можно по формуле:

\(S=\frac12a\times b\times\sin\alpha\)

где a и b — стороны фигуры, а α — угол между ними.

Через радиус описанной окружности и три стороны

Если вам известен радиус окружности, которая описана вокруг вашего треугольника, а также все его стороны, можно вычислить S следующим образом:

\(S=\frac{a\times b\times c}{4\times R}\)

где a, b и c — стороны фигуры, а R — радиус описанной окружности.

Через радиус вписанной окружности и три стороны

В случае, если вам известны все три стороны и радиус вписанной в треугольник окружности, можно найти его площадь по формуле:

\(S=r\times\frac{a+b+c}2\)

где r — радиус вписанной окружности, \(\frac{a+b+c}2\) — полупериметр фигуры.

Таким образом, формулу можно выразить всего двумя множителями:

\(S=r\times p\)

где p — полупериметр треугольника.

Через сторону и два угла

Если в данной фигуры вам известна лишь одна сторона и две прилегающих к ней угла, ее S можно найти следующим образом:

\(S=\frac12\times a^2\times\frac{\sin\alpha\times\sin\beta}{\sin\gamma}\)

причем \(\gamma=180^\circ-(\alpha+\beta)\)

Доборные элементы

Расчет дополнительной фурнитуры

Для полноценного монтажа необходима дополнительная фурнитура, так называемые доборные элементы. Такие детали можно приобрести как дополнительно, так и в комплекте с металлочерепицей. В первую очередь они необходимы для надежности кровли, в особенно ненадежных местах, а уже потом их можно рассматривать как часть декорации.

Элемент можно купить в среднем – 200 рублей за погонный метр. Но нужно подумать, что нам необходимо и для чего, а также подсчитать, во сколько это обойдется, в случае если придется покупать.

Итак, рассмотрим, нам необходимо:

1. Конек, планки торцевые, которые будут защищать от атмосферных явлений – дождь, ветер, и планка примыкания – для дополнительной герметизации различных стыков, к примеру, печной трубы. И это только самое необходимое, есть еще другие дополнительные детали, и они особенно необходимы, если система кровли сложная, многоскатная.
2. Барьер снеговой – для защиты водостока от внезапного обрушения снега, карнизная планка – защищает от попадания под конек пыли и грязи. Мы сейчас рассмотрим, как подсчитать самые необходимые комплектующие элементы, а потом исходя из расчетов, вы окончательно решите, что приобретать. Чтобы подсчитать количество фурнитуры нужно:
   • измерить длину конька, все будет зависеть, каких размеров будут планки, так как на стыки уходит 10 см, стандартный конек – 2 метра, к примеру, если длина конька 6 м, то понадобится покупать 4 планки, а это 800 рублей;
3. торцевые планки выпускаются разной длины, так и монтируются на торцевых скатах, высчитывается аналогичным образом, то есть с учетом, что на стыки должно уходить 10 см;
4. планка примыкания – рассчитывается по описанному выше принципу.

Кроме этого, необходимы саморезы стоимость их варьируется от 3 до 7 рублей за штуку. После подсчетов, можно подумать о цвете, если вы хотите, чтобы ваш дом выделялся и был виден издалека, то выбирайте любой яркий цвет. Качественно выполненная черепица не выгорает на солнце и не теряет своих качеств, и вы можете не беспокоиться, что со временем ваша крыша потеряет свой первоначальный вид.

Площадь треугольника. Онлайн-калькулятор

Онлайн-калькулятор для расчета площади треугольника поможет Вам найти площадь треугольника несколькими способами в зависимости от известных данных. Наш калькулятор не просто рассчитает площадь треугольника, но и покажет подробное решение, которое будет показано под калькулятором.

Поэтому данный калькулятор удобно использовать не только для быстрых расчетов, но и для проверки своих вычислений.

С помощью данного калькулятора вы сможете найти площадь треугольника по следующим формулам: через основание и высоту, через две стороны и угол, по трем сторонам (формула Герона), через радиус вписанной окружности, через радиус описанной окружности.

Треугольник – это геометрическая фигура, которая образована тремя отрезками. Эти отрезки называются сторонами треугольниками, а точки соединения отрезков – вершинами треугольника.

В зависимости от соотношения сторон треугольники бывают нескольких видов: равнобедренный треугольник (две стороный треугольника равны между собой, эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонний треугольник (у треугольника все три стороны равны), прямоугольный треугольник (один угол треугольника прямой).

Как найти площадь треугольника?

Найти площадь треугольника очень просто, достаточно воспользоваться нашим калькулятором или рассчитать самостоятельно, воспользовавшись формулой площади треугольника. В зависимости от того, какие данные известны, для расчета площади треугольника использует несколько способов:

1) через основание и высоту

2) через две стороны и угол

3) По трем сторонам. Формула Герона

4) Через радиус вписанной окружности

a, b, с – стороны треугольника, p – полупериметр треугольника,

r – радиус вписанной окружности.

5) Через радиус описанной окружности

a, b, с – стороны треугольника,R – радиус описанной окружности.

Вы всегда сможете проверить правильность расчета площади треугольника с помощью нашего калькулятора.

Прямоугольный треугольник и его площадь.

Прямоугольный треугольник – это треугольник, у которого один угол равен 90 градусам (потому называется прямым). Прямой угол образуют две перпендикулярные линии (в случае с треугольником – два перпендикулярных отрезка). В прямоугольном треугольнике прямой угол может быть только один, т.к. сумма всех углов одного любого треугольника равна 180 градусам. Получается, что 2 других угла должны делить между собой оставшиеся 90 градусов, например 70 и 20, 45 и 45 и т.д. Итак, основное вы вспомнили, осталось узнать, как найти площадь прямоугольного треугольника. Представим, что перед нами вот такой прямоугольный треугольник, и нам необходимо найти его площадь S.

1. Самый простой способ определения площади прямоугольного треугольника высчитывается по следующей формуле:

В нашем случае, площадь прямоугольного треугольника равна: S = 2,5 см. * 3 см. / 2 = 3,75 кв.см.

В принципе, больше нет необходимости выверения площади треугольника иными способами, т.к. в быту пригодится и поможет только этот. Но существуют и варианты измерения площади треугольника через острые углы.

2. Для других способов вычисления необходимо иметь таблицу косинусов, синусов и тангенсов. Посудите сами, вот какие варианты вычисления площадей прямоугольного треугольника еще можно использовать:

Мы решили воспользоваться первой формулой и с небольшими помарками (чертили в блокноте и использовали старую линейку и транспортир), но у нас вышел верный расчет:

S = (2,5*2,5)/(2*0,9)=(3*3)/(2*1,2). У нас вышли такие результаты 3,6=3,7, но с учетом сдвига клеток, этот нюанс нам можно простить.

Онлайн калькулятор

Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• длины катетов a и b
• длину гипотенузы с и длину любого из катетов (a или b)
• длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
• длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• длину гипотенузы с и один из острых углов (α или β)

Найти площадь прямоугольного треугольника по двум катетам

Катет a = Катет b = S =

Просто введите длины двух катетов, и получите ответ.

Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?

S = ½ ⋅ a ⋅ b

Пример

К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:

S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²

Найти площадь прямоугольного треугольника по катету и гипотенузе

Гипотенуза c = Катет (a или b) = S =

Введите длины гипотенузы и одного из катетов, и получите ответ.

Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?

S = ½ ⋅ a ⋅ √c² — a² = ½ ⋅ b ⋅ √c² — b²

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:

S = 2 ⋅ √5² — 2² / 2 = √25 — 4 ≈ 4.58 см²

Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу

Катет (a или b) = Прилежащий угол (β или α) = ° S =

Введите длину одного из катетов и прилежащий к нему острый угол в градусах.

То есть к катету a прилежащий ∠β, а к катету b — ∠α

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?

S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:

S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²

Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу

Катет (a или b) = Противолежащий угол (α или β) = ° S =

Введите длину одного из катетов и противолежащий к нему острый угол в градусах.

То есть к катету a противолежащий ∠α, а к катету b — ∠β

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?

S = ½ ⋅ a² ⋅ tg(90 — α) = ½ ⋅ b² ⋅ tg(90 — β)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:

S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:

S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²

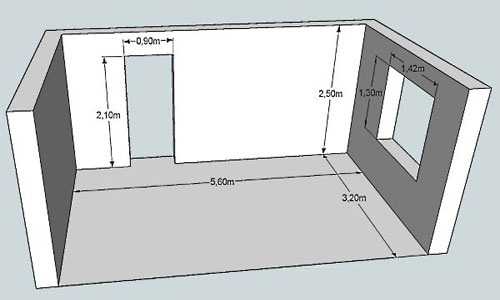
Как посчитать площадь стен

Чтобы определить площадь стен, нужно знать, как рассчитать периметр комнаты. Определение площади часто требуется для закупки всевозможных материалов для отделки. Кроме длины и ширины помещения, понадобится выяснить высоту комнаты, а также габариты проемов двери и окон.

При расчетах стоит учитывать, что высота потолков даже в одном помещении может варьироваться, особенно если комната мансардного типа. Отдельно вычисляются значения всех стен, а затем их них отнимаются оконные и дверные проемы.

Точные значения можно выявить с помощью калькулятора расчета площади стен комнаты. Иногда требуется определить объем помещения. В такой ситуации необходимо перемножить три значения: длину, ширину и высоту комнаты. Данный показатель меряется в кубических метрах.

Если помещение имеет разноуровневое зонирование, то можно провести такие расчеты:

• померить все участки стен. Замеры рекомендуется выполнять поближе к потолку;
• вычислить показатели площади по полу;
• на каждом вертикальном участке необходимо промерить длину и высоту, а затем данные значения перемножить;
• прибавьте показатели к значению пола.

У каждой комнаты есть оптимальные параметры, которые можно учитывать при планировке строительного объекта. Минимальный показатель жилого помещения равняется 8 кв. м. Комната общего назначения, такая как зал или гостиная может иметь площадь от 14 до 25 кв. м. Минимальный показатель высоты помещения составляет 240 см. Если потолок более трех метров, то такое пространство сложнее обогревать. Кухня должна иметь площадь не менее 6 кв. м.

Правильное вычисление площади помещения является гарантией качественного проведения ремонта. Такой подход позволит свести к минимуму затраты на приобретение материалов.

Ремонт – дело хлопотное, но приятное, ведь после него квартира или частный дом становятся более уютными, современными, располагающими к отдыху. «Как рассчитать площадь комнаты и стен?» – это, пожалуй, один из первых вопросов, которые возникают на горизонте переделок.

Можно не заниматься расчетами самостоятельно, а доверить это дело бригаде отделочников, которые и будут проводить ремонт. А что делать, если решение принято, и все работы будут выполняться своими руками? В этом случае расчет должен быть особо тщательный, так как отсутствие опыта может стать результатом нехватки или переизбытка того или иного материала.

Площадь комнаты в квадратных метрах

Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:

• Рулетка. Лучше — с фиксатором, но подойдет и обычная.
• Бумага и карандаш или ручка.
• Калькулятор (или считайте в столбик или в уме).

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м.  В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

Площадь комнаты сложной формы

Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):

1. Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
2. Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
3. Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту

Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный

Как посчитать площадь комнаты неправильной формы

В этом случае порядок вычислений такой:

1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
2. Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
3. Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
4. Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

Формулы расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка

Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

Задача. Найти площадь по двум сторонам и углу между ними

Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника.

Решение.

Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ

Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60   

В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов. Он будет равен корню из трех на два. 
S = 15 √3 / 2

Ответ: 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)

Вычисляем метраж

Основные этапы работы:

1. Расчет производится вдоль стен комнаты. Поэтому предварительно рекомендуется освободить их. Для этого нет необходимости полностью освобождать комнату. Во многих случаях достаточно лишь отодвинуть предметы к центру помещения.
2. Измерение значения длины стены. Для этого понадобится рулетка. Ее прикладывают к углу одной из стен и закрепляют. Ведя рулетку вдоль стены до ее конца, находят значение длины.
3. Полученное значение следует записать на листе бумаги.
4. Таким же образом необходимо найти длину второй стены.
5. Полученные в результате измерения данные следует умножить между собой. Для этого можно воспользоваться калькулятором.

Найденные данные и являются метражом комнаты.

Чтобы найти площадь комнаты, не обязательно прибегать к услугам специалистов. Процедура достаточно проста и вполне доступна каждому. Следуя предложенным рекомендациям, можно без особых усилий и в короткие сроки получить необходимые значения площади помещения.

Начиная любой ремонт, вам нужно знать, как рассчитать площадь комнаты. Эти знания помогут вам подобрать правильное количество материалов, а также грамотно просчитать габариты. Такие знания необходимы и при приобретении недвижимости, когда нужно проверить указанную в документах площадь.

Наш обзор поможет вам вспомнить школьные знания и подскажет, как применить их на практике. Кроме того, вы сможете воспользоваться специальным калькулятором.

При расчете площадей потолка, пола и стен, необходимо выяснить, как рассчитать квадратный метр. Для вычислений необходимо выбрать мерную ленту или рулетку с нанесением делений в сантиметрах или метрах. Такое приспособление применяются для площади в квадратных метрах.

Если величина получается больше метра, то используются не только метры, но и сантиметры.

Чтобы правильно провести расчеты можно воспользоваться калькулятором квадратных метров. При необходимости померить всю длину, можно делать это поэтапно. Например, сделать отметку там, где закончилась рулетка, а затем протянуть ее еще раз.

Ширина меряется также рулеткой. При этом ее располагают под углом в 90 градусов к длине. Если длина меньше метра, то необходимо округлить в сторону ближайшего сантиметра.

При расчете квадратных метров калькулятором, не всегда получается выполнить измерения в метрах. Показатель отображается, как в метрах, так и в сантиметрах. При этом 1 см равняется 0,01 метра. Например, 98 см равно 0,98 м. То есть можно записать 2,98 м. Чтобы получить площадь нужно длину умножить на ширину. Округлять значение можно в большую сторону.

Стоит отметить и другие единицы измерения:

• в 1 квадратном фунте – 0,093 квадратных метра;
• в ярде – 0,84 кв. м.

требуется точный расчет материалов для ремонта;
наемные мастера часто проводят расчеты оплаты за квадратный метр, что необходимо перепроверять для исключения обмана;
необходимы знания расчетов при выборе площади

Часто оплата коммунальных услуг вычисляется, исходя из размеров комнаты;
чтобы определить нормативы освещенности также нужно знать габариты помещения;
зная площадь, всегда можно посчитать объем, что очень важно при установке отопительных, вентиляционных и климатических устройств.. В ролике дается простое объяснение необходимых значений:

В ролике дается простое объяснение необходимых значений:

Вычисления с помощью окружностей

На практике используются способы расчета площади треугольника с помощью вписанной или описанной окружности. В первом случае необходимо знать величины всех сторон и радиус вписанного элемента. Далее:

• найдите полупериметр (p);
• умножьте полученную величину на значение радиуса (r) окружности и получите площадь.

Совет. При неизвестном радиусе его рассчитывают по формуле: r = P/2π. P — длина окружности, π — математическая константа.

По описанной вокруг треугольника окружности также можно вычислить его площадь. Потребуется знать радиус:

• получите произведение всех сторон треугольника;
• умножьте радиус на 4;
• разделите первое значение на второе.

Важно! Формула:

Пример для треугольника со сторонами 3,4 и 5 см. Если описать окружность, касающуюся каждой его вершины, то ее радиус будет равняться 2,5. После подстановки величин в уравнение получите итоговое значение 6 см2.

Предложенный набор методов — базовый, но вовсе не исчерпывающий. Существуют более сложные способы решения задания с меньшим количеством вводных данных и многоступенчатым расчетом.

3 Как вычислить площадь равнобедренного треугольника

Равнобедренным называется такой треугольник, который имеет две равные стороны. Эти стороны называются боковыми, а другая сторона является основой. Для вычисления площади равнобедренного треугольника можно использовать одну из следующих формул.

S=h*c/2,
где с – это основание треугольника, h-это высота треугольника, опущенного к основанию.

Формула равнобедренного треугольника по боковой стороне и основанию

S=(c/2)* √(a*a – c*c/4),
где с – основание треугольника, a- величина одной из боковых сторон равнобедренного треугольника.

Как найти площадь равностороннего треугольника

Равносторонний треугольник – это такой треугольник, у которого все стороны равны. Для вычисления площади равностороннего треугольника можно использовать следующую формулу:
S = (√3*a*a)/4,
где a-это длина стороны равностороннего треугольника.

Площадь треугольника

Треугольник имеет три угла или вершины, и три стороны, которые являются прямыми отрезками.

Равносторонним треугольником является треугольник, который имеет равную длину всех трех сторон.

Если две стороны треугольника и два прилегающих к ним угла равны между собой — такой треугольник называется равнобедренным

Формулы площади треугольника:

• Площадь треугольника = a * h/2
• Периметр треугольника = a + b + c
• Площадь равностороннего треугольника = (√(3) / 4) * a²
• Площадь равнобедренного треугольника = ½ * a * b * SinC

где,

• h — высота треугольника,
• a, b, c = стороны треугольника

Примеры :

Задача 1: Найдите площадь треугольника у которого высота = 3, а длина основания = 4.Шаг 1: Найдем площадь.Площадь = h * b/2 = 3 * 4/2 = 12/2 = 6.

Задача 2: Найдите периметр треугольника, если известна длина его трех сторон = 1, 2, 3.

Шаг 1: Найдем периметр.Периметр = a + b + c = 1 + 2 + 3 = 6.

Задача 3: Найдите площадь равностороннего треугольника, если длина его стороны равна 3.

Шаг 1: Найдем площадь.Площадь = (√(3) / 4) * a² = (1.73 / 4) * 3² = 0.43 * 9 = 3.87.

Задача 4: Найдите площадь равнобедренного треугольника если сторона его равна 3, основание = 4 и угол между ними 28.

Шаг 1: Найдем площадь.Площадь = ½ * a * b * SinC = 0.5 * 3 * 4 * Sin(28) = 6 * 0.27 = 1.62.

Приведенные выше примеры показывают, как вычислить площадь и периметр треугольника, равностороннего треугольника,равнобедренного треугольника вручную.

Расчет веса металла

Металл получил достаточно широкое применение в различных отраслях промышленности. Создавая металлические конструкции необходимо предварительно рассчитать два таких важных показателя: прочность, общий вес.

Прочность конструкции может быть рассчитана по методикам теории сопротивления материалов. Вес рассчитывается с учётом следующих характеристик:

• стандартная плотность образца (определяется по физическим характеристикам);
• форма металла (согласно существующего сортамента – листовой прокат, швеллер, уголок, труба, так далее);
• геометрическая форма, размеры детали.

Расчет веса металла

Наличие многообразных форм металлических изделий требует индивидуального подхода при проведении расчёта следующих параметров:

• массы всей металлической конструкции;
• необходимый объём металла.

Что такое переводной коэффициент?

Он позволяет рассчитать вес изделий из любого материала. Его получают, как отношение плотности выбранного материла к значению плотности стали. Далее для вычисления искомого параметра достаточно вычислить такой параметр стального изделия заданной формы. Полученный результат умножит на переводной коэффициент для данного материала.

Коэффициент является безразмерной величиной. Имеет свои конкретные значения у различных металлов и сплавов. Например, алюминий имеет 0,34, медь – 1,14, к бронзе марки ОЦС5-5-5 применяют 1,12.

Чтобы вычислить вес листа из указанной бронзы необходимо получить параметр такого же листа из стали, перемножив с переводным коэффициентом.

Такую же методику расчёта, применение переводного коэффициента, справедливо применять к неметаллическим изделиям прямоугольной формы. Например, к текстолиту с коэффициентом 0,18, органическому стеклу – 0,15. Полученные результаты будут удовлетворять требованиям по точности.

Чем усложняется расчёт веса металла?

Серьёзным различием в полученных данных по расчёту массы стального изделия является технология его производства. Разница между холоднокатаным прокатом металла и горячекатаным может быть достаточно существенная. Речь идет о точности геометрических характеристик при сохранении плотности по всей протяжённости изделия.

Равнобедренный треугольник и его площадь.

Если перед вами стоит задача вычислить формулу равнобедренного треугольника, то проще всего воспользоваться главной и как считается классической формулой площади треугольника.

Но для начала, перед тем, как найти площадь равнобедренного треугольника, узнаем, что это за фигура такая. Равнобедренным треугольником называется треугольник, у которого две стороны имеют одинаковую длину. Эти две стороны называются боковыми, третья сторона называется основанием. Не путайте равнобедренный треугольник с равносторонним, т.е. правильным треугольником, у которого все три стороны равны. В таком треугольнике нет особых тенденций к углам, точнее к их величине. Однако углы у основания в равнобедренном треугольнике равны, но отличаются от угла между равными сторонами. Итак, первую и главную формулу вы уже знаете, осталось узнать, какие еще формулы определения площади равнобедренного треугольника известны:

Как вы можете заметить, в этих формулах активно используются углы, их величины, косинусы, синусы и тангенсы. По этой причине, без специальной книжки вам не обойтись, хотя всю информацию вы сможете найти в Интернете. Отметим только, что в формулах угол альфа – тот, что находится между боковой стороной и основанием, а угол гамма (y) – тот, что находится между равными боковыми сторонами треугольника.

Примеры решения задач

Разберемся с нахождением площади треугольника наглядно на примере некоторых случаев.

Задача 1

В треугольник вписана окружность с радиусом 6 см. Известно, что его стороны равны 10 см, 12 см и 14 см. Определить площадь фигуры.

Решение

Для расчета будем использовать формулу \(S=r\times\frac{a+b+c}2\) или \(S=r\times p\). Подставляем имеющиеся значения и получается:

\(S=6\times\frac{10+12+14}2=6\times18=108\) \(см^2\)

Ответ: \(108\) \(см^2\).

Задача 2

Дан равносторонний треугольник, вокруг которого описали окружность с радиусом 3 см. Посчитать S данной фигуры.

Решение

Считать будем, опираясь на следующее уравнение \(S=\frac{3\sqrt3R^2}4\). Подставляем данные величины и получаем:

\(S=\frac{3\sqrt33^2}4=\frac{27\sqrt3}4 см^2\)

Ответ: \(\frac{27\sqrt3}4 см^2.\)

Задача 3

Известно, что у равнобедренного треугольника основание равно 4 см, а стороны по 3 см. Нужно вычислить площадь фигуры.

Решение

Для расчета S используем формулу \(S=\frac b4\sqrt{4a^2-b^2}\). Получается:

\(\frac44\sqrt{4\times3^2-4^2}=\sqrt{36-16}=\sqrt{20}=2\sqrt5 см^2\)

Ответ: \(2\sqrt5 см^2.\)

Задача 4

Дан треугольник с прямым углом, у которого гипотенузы равна 2 см, а один из острых углов равен \(30^\circ\). Узнать S данной фигуры.

Решение

Для расчетов будем ориентировать на следующее уравнение: \(S=c^2\times\cos\left(\alpha\right)\times\sin\left(\alpha\right)\). Подставляем известные значения:

\(S=2^2\times\frac{\sqrt3}2\times\frac12=\sqrt3 см^2\)

Как узнать площадь окон и дверей?

Площадь, занятая окнами, измеряется по откосам и подоконнику. Высота окна определяется по боковому откосу, ширина – по подоконнику или верхнему откосу.

Например, ширина окна – 1,55 м, высота – 1,65 м.

1,65 х 1,55 = 2,56 м2

Если окон несколько, общая площадь их суммируется.

Площадь треугольного окна: S = 0,5А*h, где А – нижняя сторона/ширина окна, h – высота.

Если ширина треугольного окна 2 метра, а высота – 1,5 метра, то площадь окна составит:

0,5 х 1,5 х 2 = 1,5 м2.

Площадь дверей, также как и площадь прямоугольной стены, измеряется простым умножением ширины двери на высоту. За основу берутся снятые замеры по коробке, а не по полотну.

Вы здесь

Онлайн калькулятор — Учеба и наука — Математика — Геометрия — Геометрический калькулятор — Треугольник

Треугольник

Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.

Зная: Стороны треугольника	Зная: Два угла и сторону треугольника	Зная: Два угла и сторону треугольника «A»
Зная: Две стороны и угол треугольника	Прямоугольный треугольник	Зная: Катет и гипотенуза прямоугольного треугольника
Катет «B» и гипотенуза прямоугольного треугольника	Зная: Катет и угол прямоугольного треугольника	Катет «A» и угол «β» прямоугольного треугольника
Катет «B» и угол «α» прямоугольного треугольника	Катет «B» и угол «β» прямоугольного треугольника	Зная: Гипотенузу и угол прямоугольного треугольника
Гипотенуза и угол «β» прямоугольного треугольника	Равнобедренный треугольник	Зная: Высоту и сторону равнобедренного треугольника
Высота и сторона «B» равнобедренного треугольника	Зная: Сторону и угол равнобедренного треугольника	Сторона «A» и угол «β» равнобедренного треугольника
Сторона «B» и угол «α» равнобедренного треугольника	Сторона «B» и угол «β» равнобедренного треугольника	Зная: Высоту и угол равнобедренного треугольника
Высота и угол «β» равнобедренного треугольника	Равносторонний треугольник	Зная: Площадь равностороннего треугольника
Зная: Высоту равностороннего треугольника	Зная: Радиус вписанной окр. равностороннего треугольника	Зная: Радиус описанной окр. равностороннего треугольника
Зная: Основание и высоту треугольника