Фигура треугольник в техническом анализе: стратегия торговли

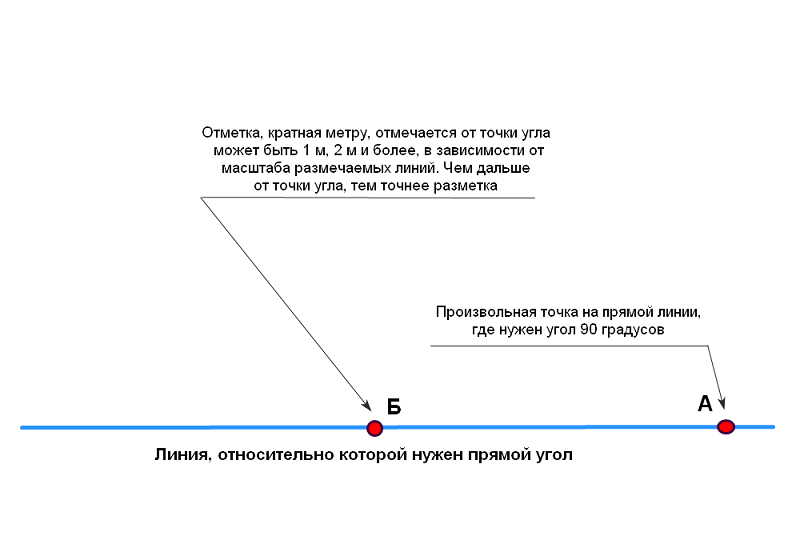
Иные способы выведения прямого угла

Если нет желания заниматься выведением углов самостоятельно, а финансы позволяют обратиться за помощью к специалистам, можно вообще не думать об этом вопросе. Один звонок − и на участке уже находится геодезист с теоделитом, который в сжатые сроки сделает разметку. Однако в этом случае необходимо быть готовым к внушительным затратам на оплату его труда.

ФОТО: omegagalvanoplastia.com.brТеоделит – высокоточная техника, однако стоимость подобной разметки может влететь «в копеечку»

Если говорить о минимальных затратах, то, основываясь на прайс-листах фирм, оказывающих подобные услуги, вызов и работа геодезиста с инструментом обойдётся в 1 000 руб./час при минимальной оплате 7 000 руб. Дальше − больше. Разметка осей (2 точки) – ещё 3 000 рублей. Если же потребуется определить точные координаты по GPS, то здесь каждые три точки обойдутся владельцу в 5 000 руб. Можно посчитать, какова будет общая сумма (все цены указаны с учётом на конец сентября 2020 года). Не проще ли самому произвести все необходимые разметки? Ведь сэкономленные средства всегда можно потратить на что-то полезное в дальнейшем строительстве.

ФОТО: thelundreport.orgСтоит приготовиться к тому, что карман значительно облегчится

Свойства равностороннего треугольника:

1. В равностороннем треугольнике все стороны равны между собой.

2. В равностороннем треугольнике углы равны и составляют 60°.

3. В равностороннем треугольнике каждая медиана, проведенная к каждой стороне, является биссектрисой и высотой, и они равны между собой.

В равностороннем треугольнике биссектриса, проведенная к каждой стороне, является медианой и высотой, и они равны между собой.

В равностороннем треугольнике высота, проведенная к каждой стороне, является биссектрисой и медианой, и они равны между собой.

Рис. 2. Равносторонний треугольник

АK = BF = CD

4. В равностороннем треугольнике высоты, биссектрисы, медианы и серединные перпендикуляры пересекаются в одной точке, которая называется центром равностороннего треугольника. Она же является центром вписанной и описанной окружностей.

Рис. 3. Равносторонний треугольник

R – радиус описанной окружности, r – радиус вписанной окружности

5. В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной.

6. Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, если считать от вершин.

Рис. 4. Равносторонний треугольник

AO : OK = BO : OА = CO : OD = 2 : 1

Средневековье

Ранние христиане образ Бога графически обозначали треугольником, изображения которого можно видеть в римских катакомбах и погребальных плитах. После Первого Вселенского собора (325 г.), на котором была утверждена формула вероисповедания, церковь адаптировала некоторые из древних знаков в качестве христианской символики.

До десятого века не принято было изображение трех ипостасей (ликов) единого Бога, а именно Отца, Сына, Святого Духа в человеческих образах. Потому такие фигуры, как трикветр, стилизованный трилистник, трискелион, простой и образованный из различных элементов треугольник, а также иные знаки стали знаменовать Святую Троицу.

Какой-нибудь древний символ триединства превращался в декоративный элемент храмовой архитектуры и богато иллюстрированной библии. Подобные знаки появлялись на фресках и в религиозной живописи, в качестве украшений и защитных амулетов на рыцарских щитах, оружии, доспехах, а также на родовых гербах.

Какие бывают геометрические фигуры?

Какие бывают геометрические фигуры?

• В сферу изучения науки геометрии входят плоские (двухмерные) фигуры и объмные фигуры (трхмерные).

  Из плоских:

  Их изучает планиметрия. Точка тоже плоская фигура.

  Из объмных известны:

  Их изучает стереометрия.

• К фигурам также относится и точка.

  Трехмерные фигуры — куб, сфера, полусфера, конус, цилиндр, пирамида, параллелепипед, призма, эллипсоид, купол, тетраэдры и множество других, выходящие из вышеуказанных. Далее идут очень сложные геометрические фигуры — различные многогранники, которые по сути могут содержать бесконечное количество граней. Например, большая клинокорона — состоит из 2-х квадратов и 16-ти правильных треугольников или клинокорона, составленная из 14 граней: 2 квадрата и 12 правильных треугольника.

• Говоря о геометрических фигурах, можно выделить такие две закономерные группы как:

  1) Двухмерные фигуры;

  2) И трхмерные фигуры.

  Итак, поподробнее о двухмерным, к ним можно отнести такие фигуры как:

  А вот что касается трхмерных фигур, то вот какими они могут быть:

• Очертания фигур и все возможные действия с ними изучают математические науки геометрия (изучает плоские фигуры) и стереометрия (предмет изучения — объемные фигуры). Я в школе любила и ту, и другую науку.

  Вот так классифицируются плоские (2D) фигуры:

  **

  Объемные фигуры (3D) классифицируются таким образом:

  **

  Это куб, параллелепипед, тетраэдр, цилиндр, пирамида, икосаэдр, шар, додекаэдр, конус, октаэдр, призма, сфера. К тому же есть усеченные фигуры (пирамида, конус). В зависимости от основания, пирамида, призма делятся на треугольные, четырехгранные и так далее.

  Детские игрушки (пирамидки, мозаика и другие) позволяют с раннего детства знакомить детей с геометрическими объемными фигурами. А плоские фигуры можно нарисовать и вырезать из бумаги.

• Из двухмерных можно назвать следующие:

  • круг;
  • овал;
  • квадрат;
  • прямоугольник;
  • параллелограмм;
  • трапеция;
  • пятиугольник (шестиугольник и т.д.);
  • ромб;
  • треугольник.

  С трехмерными немного посложнее:

  • куб;
  • цилиндр;
  • конус;
  • призма;
  • сфера или шар;
  • параллелепипед;
  • пирамида;
  • тетраэдр;
  • икосаэдр;
  • октаэдр;
  • додекаэдр.

  Думаю многие, прочитав последния названия, спросили про себя: quot;Что-что?quot;. Для наглядности — иллюстрация:

• На самом деле фигур в математике достаточно. Плоские фигуры это — прямоугольники, квадрат, треугольник, пятиугольник, шестиугольник, круг. Объемные фигуры или 3D фигуры — это как пирамида, так и куб и додекаэдр, и тд.

• 1 Из двухмерных фигур:

  2 Из трхмерных фигур:

  Призма, пирамида, параллелепипед, призма, шар (сфера), цилиндр, полусфера (половинка от сферы, то есть шар, разрезанный пополам) и конус. Пирамиды делятся на треугольные, четырхугольные и так далее (почти до бесконечности). Чем больше у пирамиды углов в основании, тем больше она напоминает конус.

• Трхмерные фигуры (3D): двугранный угол, многогранный угол; многогранник (разновидности многогранников: призма разновидности призмы: параллелепипед, куб, антипризма, пирамида разновидность тетраэдр, усечнная пирамида, бипирамида разновидность октаэдр, додекаэдр, икосаэдр, клин, обелиск); цилиндр, усечнный цилиндр, отрезок цилиндра (он же цилиндрическая подковка или quot;копытоquot;), конус, усечнный конус, сфера, шар, шаровой сегмент, шаровой слой, шаровой сектор, эллипсоид, геоид…

• С самого начала мы на уроках геометрии изучаем простые фигуры, которые являются плоскими, то есть располагаются на одной плоскости.

  Далее, перед нами открывается мир объмных фигур, которые необходимо представлять и понимать, как они расположены и как грамотно их нарисовать, чтобы было понятно не только вам, но и окружающим.

  Итак, перечень основных фигур можно изучить ниже.

• В последнее время мне как раз приходилось рассказывать своим внучкам и внуку, какими могут быть геометрические фигуры.

  Начинали с плоских фигурок, вырезанных из картона или сделанные из пластмассы, дети учились различать треугольник и квадрат, овал и круг, прямоугольник, ромб и многоугольник.

  Помогали в запоминании названий фигур и вот такие специальные игрушки с отверстиями определнной формы.

  Позднее перешли на объмные фигурки, кубики и конусы, параллелепипеды, шары и кольца, пирамидки и цилиндры.

  До школы они пока не доросли, а когда пойдут, то их научат различать равнобедренные и равносторонние треугольники, узнают про луч и точку, про окружность и вс остальное.

Точка пересечения биссектрис треугольника

Теорема 2

О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

Рассмотрим треугольник $ABC$, где $AM,\ BP,\ CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM\ и\ BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

Рисунок 2. Биссектрисы треугольника

Для доказательства нам потребуется следующая теорема.

Теорема 3

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

По теореме 3, имеем: $OX=OZ,\ OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.

Теорема доказана.

Бычий и медвежий вымпел

Вымпелы на графике имеют форму, аналогичную форме симметричных треугольников. Они обычно появляются во время трендов и имеют характер продолжения тренда.

Бычий вымпел похож на симметричный треугольник по внешнему виду, но его происходит после повышения цены. Поскольку вымпелы имеют характер продолжения тренда, бычий вымпел, скорее всего, продолжит текущий бычий тренд на графике. Когда верхняя сторона вымпела пробивается вверх, мы, вероятно, увидим движение цены, равное, по крайней мере, размеру вымпела.

При торговле вымпелами можно использовать вторую цель фиксации прибыли, чтобы получить большую прибыль. При расчете второй цели вы должны проанализировать движение цены. Вы можете установить цель 1:1 предыдущего этапа или 0,618. Когда тренд кажется сильным и имеет крутой уклон, движение 1: 1 будет подходящей второй целью, и во всех других случаях можно использовать 0,618.

Медвежий вымпел является зеркальным отражением бычьего вымпела. Медвежьи вымпелы начинаются со снижения цены и заканчиваются симметричным появлением треугольника. Поскольку вымпелы имеют тенденцию продолжения тренда, медвежьи вымпелы продолжат медвежий тренд.

Когда цена проходит через нижний уровень медвежьего вымпела, вы должны сначала попытаться захватить первую цель, которая равна размеру самого вымпела. Когда цена достигает этой цели, вы можете попытаться поймать дальнейшее снижение, которое равно размеру предыдущего этапа или 0,618.

Прямоугольный треугольник

В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла. 

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$. (Рис.14)
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника. (Рис.14)

Один острый угол прямоугольного треугольника на $44°$ больше другого острого угла. Найдите больший острый угол.

Решение:

В прямоугольном треугольнике $АВС$ $∠А$ и $∠В$ – острые.

Пусть $∠ А – х$, тогда $∠ В — (х+44)$.

Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

На основании этого правила, составим и решим уравнение:

$х+х+44=90$

$2х+44=90$

$2х=90-44$

$2х=46$

$х=23$

Угол $В$ больший в этом треугольнике, через $«х»$ он записывался как, $х+44$, следовательно, $∠В=23+44=67°$.

Ответ: $67$

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. 

$АС^2+ВС^2=АВ^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$ 

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
5. Основное тригонометрическое тождество: $sin^2x+cos^2x=1$
6. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
7. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
8. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Элементы остроугольного треугольника:

Кроме сторон и углов у одностороннего треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. остроугольного, 6 внешних углов, по 2 на каждый внутренний. Любой внешний угол остроугольного треугольника всегда будет тупым углом.

Рис. 4. Остроугольный треугольник и внешний угол

∠ ВСD – внешний угол

Медиана остроугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 5. Остроугольный треугольник и медиана остроугольного треугольника

MС – медиана остроугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 6. Остроугольный треугольник и высота остроугольного треугольника

MС – высота остроугольного треугольника

Высота остроугольного треугольника находится внутри треугольника. Все 3 высоты остроугольного треугольника (как и любого треугольника) пересекаются в одной точке, называемой ортоцентром.

Биссектриса в остроугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы  пересекаются в точке, которая является центром вписанной окружности.

Рис. 7. Остроугольный треугольник и биссектриса угла остроугольного треугольника

MС – биссектриса угла остроугольного треугольника

Кроме того, биссектриса остроугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Египетский треугольник в строительстве

Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника. Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы

Стороны конструкции имеют следующее соотношение друг к другу:

Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

1. 5,
2. 4,

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов. Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример

Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол

Края должны совпасть.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках

Какие существуют альтернативные варианты

Как создать прямой угол

Лучшим вариантом смастерить прямой угол является применение угольника или транспортира. Это позволит с минимальными затратами найти необходимые пропорции. Но, основной момент египетского треугольника в его универсальности из-за возможности создать фигуру, не имея под рукой ничего.

В этом деле может пригодиться все, даже печатные издания. Любая книга или даже журнал имеют всегда соотношение сторон, образующее прямой угол. Типографские станки работают всегда точно, чтобы рулон, заправленный в машину резался пропорциональными углами.

Древние инженеры придумывали много способов строительства египетского треугольника и всегда экономили ресурсы.

Поэтому, самым простым и широко применяемым был метод постройки геометрической фигуры с применением обычной веревки. Бралась бечевка и резалась на 12 ровных частей, из которых выкладывалась фигура с пропорциями 3,4 и 5.

Как создать другие углы?

Египетский треугольник в строительном мире нельзя недооценивать. Его свойства однозначно полезны, но без возможности построить углы другого градуса в строительстве невозможно. Чтобы образовался угол в 45 градусов, понадобится рамка или багет, которые распиливаются под углом в 45 градусов и соединяются между собой.

Важно! Чтобы получить необходимый наклон, потребуется позаимствовать бумажный лист из печатного издания и согнуть его. Линии изгиба при этом будут проходить через угол

Края должны быть соединены.

Получить 60 градусов можно с применением двух треугольников по 30 градусов. Чаще всего используются для создания декоративных элементов.

Свойства треугольников

Введем теперь некоторые свойства треугольников в виде теорем. В данной статье доказательства их мы рассматривать не будем.

Вначале приведем теоремы, которые относятся ко всем видам треугольников. Но для них нам будут необходимы еще несколько понятий.

Определение 9

Медианой будем называть отрезок, который соединяет вершину с серединой противоположной стороны.

Определение 10

Биссектрисой будем называть луч, который проведен из вершины так, что делит угол в этой вершине на две равные части.

Определение 11

Высотой будем называть отрезок, который проведен из вершины так, что падает на противоположную сторону под прямым углом.

Теорема 1

Все три медианы в треугольнике пересекаются в единственной точке, которая будет называться центроидом треугольника.

Теорема 2

Все три биссектрисы в треугольнике пересекаются в единственной точке, которая будет называться инцентром треугольника.

Теорема 3

Все три высоты в треугольнике пересекаются в единственной точке, которая будет называться ортоцентром треугольника.

Следующие две теоремы рассматривают свойства для равнобедренных треугольников.

Теорема 4

Углы при основании равнобедренного треугольника будут равными.

Теорема 5

Высота, медиана и биссектриса в равнобедренном треугольнике являются одной и той же прямой.

Замечание 1

Отметим, что теоремы, относящиеся к равнобедренным треугольникам также справедливы и для равносторонних треугольников.

Откуда взялся символ валькнут

Валькнут, представляющий собой знак, вмещающий три треугольника, чаще всего встречается на рунических камнях, жертвенниках и изображениях битв или казней.

Также этот знак обнаруживался на ритуальных принадлежностях для погребения.

Традиционно этот символ выбивался на жертвенных камнях, предназначенных для осуществления казни «кровавый орел».

В ходе казни еще живому человеку рассекали ребра, выворачивали их в стороны и доставали легкие. Последние клали на плечи казнимому наподобие крыльев.

Такой способ казни применялся к врагам, плененным в ходе военных конфликтов, а в некоторых источниках описывается как способ мести (например, за убийство).

Это считалось принесением жертвы Одину, поэтому валькнут, как непременный атрибут такого жертвенника, и связывают с этим богом.

По значению валькнут, скорее всего, отображал некий «путь воина»: от земного существования до Вальхаллы и встречи с Одином.

Также археологи находили валькнут на оружии и доспехах. Предположительно, знак наносился также в качестве ритуальной татуировки воинам, посылаемым на смерть, то есть в бой, с которого был крайне мал шанс вернуться.

Очевидно, что таким образом воина заблаговременно готовили к загробной жизни.

Точка пересечения серединных перпендикуляров треугольника

Теорема 4

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

Пусть дан треугольник $ABC$, $n,\ m,\ p$ его серединные перпендикуляры. Пусть точка $O$ — точка пересечения серединных перпендикуляров $n\ и\ m$ (рис. 3).

Рисунок 3. Серединные перпендикуляры треугольника

Для доказательства нам потребуется следующая теорема.

Теорема 5

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.

По теореме 3, имеем: $OB=OC,\ OB=OA$. Следовательно, $OA=OC$. Значит точка $O$ равноудалена от концов отрезка $AC$ и, значит, лежит на его серединном перпендикуляре $p$.

Теорема доказана.

Троица и треугольник

Начиная с ранних христиан треугольник был символом Святой Троицы. Равносторонний треугольник толковался как равенство и единая божественная сущность Бога Отца, Бога Сына и Духа Святого. Иногда этот символ составляли из трех переплетенных между собой рыб. Символ Троицы по католической традиции составлялся из трех малых треугольников, вписанных в один большой с кругами на вершинах. Три этих круга означают триединство, но каждый круг независим и совершенен сам по себе. Эта схема иллюстрировала принцип триединства и вместе с тем индивидуальности каждого составляющего Святой Троицы.

Схема Святой Троицы по католической традиции

Треугольники как символ Троицы в готической архитектуре